表皮効果とは

金属に電流を流すと直流信号は金属の中を一様に流れ、その電流の最大値は金属の固有抵抗$\small{ρ}$と断面積$\small{S}$と長さ$\small{L}$で決まります。
即ち、抵抗値$\small{R}$は

$R = ρ \cdot \dfrac{L}{S}$

従って断面積が大きいほど抵抗値が小さくなるという性質をもっています。
では、金属に高周波信号を加えるとどうなるでしょうか。
高周波信号は周波数が高くなるに従って、導体の断面を一様には流れず、表面に近いところを密集して流れ中心部には殆ど流れません。このような現象を表皮効果と呼んでいます。これは、電流を流すとその直角方向に磁界が生じ、この磁界の密度は導体の中心部ほど強くなり、その磁界による逆起電力が発生し電流が流れるのを阻止する方向に働くからです。

川の流れを考えてみましょう。
川は川底に砂や石がごろごろしています。これらの石ころは川の流れをさえぎり、あたかも水が流れにくくなるように働きます。また、大きな石の周りには渦や淀みなどができ、このため川底に近い部分は流れが緩やかになります。一方、川の表面に近い部分では川底の影響は殆ど無くなり、早く流れていきます。これは川の表面ほど流れを遮る抵抗が小さいからなのです。

この様子は高周波の場合の表皮効果と良く似ています。高周波電流はこのように導体の表面に近いところしか流れないのです。
表皮効果は導体の表面に流れる電流の$\require{physics} \flatfrac{1}{e} \fallingdotseq 0.37$になる深さ$\small{d}$を計算します。

$d = \sqrt{\dfrac{2ρ}{ωμ}} = \sqrt{\dfrac{2}{σωμ}}$
$\small{ρ}$：導体の抵抗率
$\small{σ}$：導体の導電率 $= \require{physics} \flatfrac{1}{ρ}$
$\small{ω}$：電流の角速度 $= 2πf$
$\small{μ}$：導体の透磁率

導体が銅の場合を考えてみます。銅は非磁性体なので透磁率は空気中の透磁率とほぼ等しくなり

$μ \fallingdotseq 4π \times 10^{-7}$　(H/m)

また銅の導電率

σ＝58.1×106　(s/m）

ですので

ｆをGHｚで定義すると表皮深さdは

d≒2.09×√1/ｆ　（μｍ）

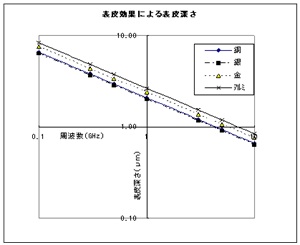
1ＧＨzでは約2μm　、10ＧＨzでは約0.7μmとなります。即ち、電流のほとんどが導体表面付近に集中していることが分かります。このことから、同軸コネクタやフィルタなどの構造体には主に加工性や強度を重視した金属で製作し、電流の集中する表面付近には、周波数による表皮効果を考慮した銀メッキなどを施す手法が用いられています。

周波数(GHz)	0.1	0.3	0.5	1	3	5	10
銅	6.61	3.81	2.95	2.0	1.21	0.93	0.66
銀	6.42	3.70	2.87	2.03	1.17	0.91	0.64
金	7.57	4.37	3.38	2.39	1.38	1.07	0.76
アルミニウム	8.37	4.83	3.74	2.65	1.53	1.18	0.84

高周波用語集》
デシベル計算｜減衰器｜固定アッテネータ抵抗値表｜終端器、抵抗整合器｜アンプの用語解説｜物理定数｜周波数と波長｜表皮効果（Skin Effect)｜損失｜リターンロス・VSWR分配・合成｜同軸切換器｜同軸ケーブル｜同軸ケーブルの呼称と標準的な規格｜同軸コネクタ｜同軸コネクタ基本構造｜雑音指数｜インピーダンスマッチング（インピーダンス整合）